In fact, it is in one sense simpler than the 15 Puzzle, because while in that other case half the configurations are unreachable, in Caboodle, any configuration is reachable from any other.
We demonstrate that below.
Lemma 1:
For any two spaces, there is another space which
is "in line" (possibly separately) with each of them.
There are two cases:
a)
the two spaces are also in line with each other, forming a "Caboodle
triangle".
Caboodle triangles can be flat (Fig 1-a) or normal (Fig 1-b).
The corners of the triangle don't have to be adjacent,
they can have one or two disks between them, forming
sides of length 3 or 4 as well.
b)
they are not on one of the lines. (Fig 2, Fig 3)
Lemma 2:
By Lemma 1, the empty space can be moved anywhere in one or two steps.
If the empty space lines up with the desired space, just move it there in one step.
If it is not, find some suitable intermediary, and use two steps.
Theorem:
Colors of any two spaces can be swapped, leaving everything else in place.Proof:
- If necessary, using Lemma 2, move the empty space so that Lemma 1a or 1b applies.
- Then swap the desired pair using one of these procedures.
- Reverse Step 1 to put the empty space back where it was.
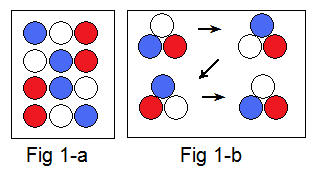
Figures 1-a and 1-b show how to use a triangle
(Lemma 1a).
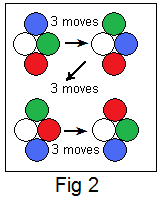
When the desired pair isn't on a line, Figure 2 shows how to use a common intermediary to do 3 swaps (9 moves), leaving blue and red interchanged.
The intermediary/ies need not be adjacent to the elements of the pair, but can be anywhere in line with them.
Figure 3 shows the same thing using two intermediaries,
and, again, 9 moves:
You want to swap blue with red.

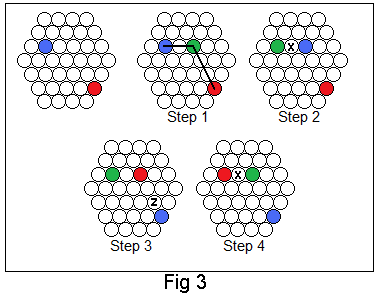
 Note that you must have the empty space at 'x' or 'z' when needed,
you might have to make more moves to get it there,
which you then reverse at the end to get it back where it was
before you started.
Note that you must have the empty space at 'x' or 'z' when needed,
you might have to make more moves to get it there,
which you then reverse at the end to get it back where it was
before you started.